17世纪的欧洲，科学与神学的角力暗流涌动。在荷兰一间狭小的病室中，一位孱弱的法国人凝视着天花板上的蛛网，思绪如银丝般延伸。蜘蛛在垂直的墙角游走，与两面墙的距离不断变化——这一瞬间的观察，竟成为数学史上最耀眼的灵感之一。这位病榻上的思想家，正是勒内·笛卡尔。他怀揣着一个宏大的野心：将几何学从图形的桎梏中解放，用代数方程重新定义空间与形式，从而统一数学的疆域。这场思维的革命，不仅催生了解析几何学，更彻底改变了人类认知世界的逻辑。

哲学与数学的交汇：笛卡尔的理性主义蓝图

笛卡尔的野心根植于其哲学体系的核心——“普遍数学”理想。他认为，真理的探索应建立在“不可怀疑”的基石上，而数学因其逻辑的纯粹性，成为唯一符合这一标准的工具。然而，传统几何学令他深感矛盾：欧几里得的演绎体系虽严谨，却过分依赖图形直觉，难以突破复杂曲线的藩篱；代数虽能机械化运算，却被符号的丛林束缚，丧失了直观性。

这种批判性思考催生了他颠覆性的洞见：几何的“形”与代数的“数”本质相通。他设想，若能用方程描述点的位置，曲线即可转化为代数关系，几何问题将迎刃而解。这一思想在1637年的《几何学》中初现雏形，书中首次提出“坐标系”概念，将平面上的点与有序数对(x,y)一一对应。正如他所述：“任何几何问题都可归结为代数方程，而解方程的过程即是对几何性质的揭示。”

坐标系的诞生：蜘蛛网上的数学诗篇

笛卡尔的突破性贡献，在于将抽象的空间关系具象为可计算的数值系统。他受航海经纬度的启发，在平面上设定两条垂直的数轴（今称笛卡尔坐标系），通过点的坐标定位，将几何图形转化为代数方程。例如，圆的标准方程x² + y² = r²，以简洁的符号语言替代了欧几里得繁琐的尺规作图，直指圆的本质——到定点距离相等的点的集合。

这一方法的革命性体现在两方面。第一方面，变量数学的曙光：坐标系引入变量概念，使静止的几何图形转化为动态的函数关系。例如抛物线y=ax²+bx+c的方程，不仅描述形状，更通过导数揭示其切线斜率的变化规律，为牛顿的微积分铺平道路。第二方面，几何难题的代数化突围：古希腊三大几何难题（三等分角、化圆为方、倍立方体）困扰学者千年，因其尺规作图的局限性无解。笛卡尔证明，这些问题的本质是代数方程的不可解性，终结了无谓的图形尝试。

皮埃尔·德·费马

解析几何的科学革命：从星空到炮弹的数学之眼

笛卡尔的野心远不止于理论建构。他将解析几何视为“自然之书”的解码器，推动科学从定性描述迈向定量分析。

• 天文学：开普勒的行星椭圆轨道定律

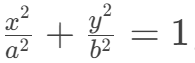
通过方程精确化，颠覆了“完美圆形”的宇宙观。

• 物理学：伽利略的抛体运动轨迹被解析为抛物线方程

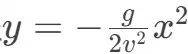
为弹道学奠定基础。

• 光学：光的折射定律

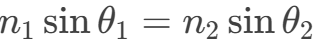
通过坐标几何得以可视化，透镜设计从此有据可循。

恩格斯评价：“数学的转折点是笛卡尔的变数。有了变数，运动进入数学；有了变数，辩证法进入数学。”解析几何将运动与变化纳入数学框架，成为微积分诞生的温床，更催生了牛顿的《自然哲学的数学原理》。

野心的边界：从万能钥匙到抽象迷宫

笛卡尔曾宣称“一切问题皆可化为方程”，这一雄心在现代数学的复杂图景中显露出局限性。20世纪霍奇猜想的提出，暴露了解析几何在高维代数簇中的无力——某些形状无法被简单几何部件组合描述，必须引入非几何的抽象模。中国数学家恽之玮等人的工作表明，即便是霍奇猜想，也需借助数论与拓扑学的跨学科工具，远非单一方程可解。

然而，这种局限恰恰印证了解析几何的深远影响：它开创的“数形互构”范式，使数学从具象走向抽象，从静态走向动态。现代代数几何中，格罗滕迪克用概形理论将几何对象抽象为交换环的谱，正是笛卡尔思想的超维延伸。

300年后，笛卡尔的墓碑上镌刻着“欧洲理性主义之父”。他的野心并未止步于坐标系的确立，而是指向更宏大的愿景——用数学构建理解世界的通用语言。今日，从人工智能的神经网络（以高维几何描述数据流）到弦理论的卡-丘流形（六维空间的代数簇），解析几何仍是科学探索的核心工具。笛卡尔的故事提醒我们：最伟大的科学革命，往往始于对常识的质疑与对统一的执着。正如那只天花板上的蜘蛛，在理性的银丝间织就的不仅是几何的坐标，更是人类向真理攀登的天梯。